Research: Baryon Acoustic Oscillations Tutorial
Pretty much everything I study in cosmology is possible because of the existence of baryon acoustic oscillations (BAO). This page is a brief, pedagogical introduction to what BAO are and why they are so important to cosmology.
On This Page: What Are Baryon Acoustic Oscillations? • Baryon Acoustic Oscillations in the Cosmic Microwave Background • Baryon Acoustic Oscillations in the Distribution of Galaxies • Credits
What Are Baryon Acoustic Oscillations? [⯅ Top]
The Universe that emerged from the Big Bang was remarkably uniform—how it got that way is a major research question, and though inflation is the most popular explanation, there are still a lot of unknowns, none of which I will go into here. The important fact for our purposes is that the ‘initial condition’ was an almost perfectly homogeneous gas of photons (or radiation), hydrogen and helium, neutrinos and dark matter. (We don't know exactly what dark matter is, but we do know that there is such a substance, and it interacts only gravitationally with the other substances.)
Drag the slider to watch how an initial point-like over-density propagates BAO as the Universe grows, i.e., as redshift, z, decreases. Note that τ is conformal time, not the age of the Universe, and the radius is in comoving coordinates. Left: Normalised profiles of CDM, mass and radiation as a function of radius. The bottom panel is the normalised over-density; the top panel has been multiplied by r2 to show the (normalised) amount of excess mass. A Hubble parameter of h = 0.7 has been used. Right: Two-dimensional slice of the density (i.e., bottom-left plot), with a logarithmic colour scale. (The small-scale graininess, which makes the figure less bland to the eye, is artificial.) This figure was made with a slightly modified version of CAMB.
The gas was almost homogeneous, but there were slight over- and under-densities sprinkled randomly throughout. Because the pressure exerted by radiation is proportional to its density, these small density variations caused pressure variations in the radiation field and this made sound waves propagate through the gas.
At high temperatures, atomic matter is ionised, meaning that the nuclei and the electrons are not bound to each other. Thus, the atomic component, or the baryons (the slightly inaccurate term commonly used in cosmology), is not electrically neutral, and because radiation interacts strongly with charged particles, the radiation and the baryons were tightly coupled together. You can roughly think of the result as a single component—a baryon-photon gas. What this implies is that the sound waves caused by the radiation pressure travelled through the baryon-photon gas.
This is the situation for the first 400,000 years or so. In Illustration 1, above, you can watch how a spherical sound wave propagates from an initial, point-like over-density. Up until about z = 1,200, the baryons and the photos rush away from the centre together, precisely because they are tightly coupled together. They are travelling at about a third the speed of light, which the speed of sound in this very dense medium. Meanwhile, the dark matter spreads out much more slowly. This is because it is not electromagnetically coupled to the photons. It only interacts gravitationally, and so it only follows slowly behind in response to the gravitational tug of the photon-baryon component.
Beginning at about z = 1,200, the Universe has cooled enough that the hydrogen and helium stops being ionised. Baryons are now neutral and stop being coupled to radiation. As you continue moving Illustration 1 forward, you see that the photons keep streaming off (now at the speed of light) and their density quickly becomes negligible. Meanwhile, the baryons no longer feel any pressure, and the baryon part of the sound wave stalls.
As the Universe continues expanding, the baryon feature, which has grown to a shell of about 150 megaparsecs in radius, persists. If you keep moving Illustration 1 forward, you see that the dark matter and the baryons gravitationally interact until the present time, when they have come to equilibrium on the large scales depicted here. (On small scales, things become very nonlinear, which introduces small modifications not captured in the Illustration.) The highest density is where the initial over-density was way back at the beginning of the Universe, because there is a lot more dark matter than baryons. But there is still a significant amount of excess mass at the 15 Mpc BAO scale. (By the way, this length scale is in comoving coordinates, i.e., the length it has in the size of the Universe today. At the time when the photons decouple, the Universe was ~1,100 times smaller, so the feature was ~140 kpc in size.)
The above is a description of how a 150 Mpc feature gets imprinted in the large-scale structure of the Universe. The next couple of sections you can see how it affects cosmological observables.
Baryon Acoustic Oscillations in the Cosmic Microwave Background [⯅ Top]
The cosmic microwave background (CMB) comes from the epoch when the baryon component of the primordial gas became neutral and the radiation could escape and free-stream. Variations in the temperature of the CMB are largely due to the density variations in the radiation at the moment it was liberated. (There are a few oversimplifications in what I've just said, but I'll bring those up later.)
Of course, the universe didn't begin with a single point-like over-density as shown in Illustration 1. Variations in the density existed everywhere. As far as we can tell, the distribution of these variations were random and Gaussian. Thus, from each point of space, a spherical shell of BAO started growing, each one with a different amplitude. All these shells intersected with each other like the growing ripples in a pond when pebbles are scattered onto the surface of the water.
A cartoon of a roughly 10×3 deg2 area showing how the CMB is composed of the superposition of lots of BAO shells. Each shell in the above illustration uses the density distribution, as shown in Illustration 1 at z = 1075, roughly the time at which the baryons and photons decoupled. The CMB density variations are mostly due to photon distribution, so we only show the photon densities without the dark matter or baryons, and this time on a linear scale. In the CMB, we see slices through shells at random positions and locations. Sometimes, as in the first frame of the above illustration, the slice is right through the middle, but a lot of slices are through other locations, including the limb. As the number of shells becomes appreciable, no single shell can be distinguished, but the resulting patterns do have a size that is roughly the size of the 150 Mpc shells.
The above is also available as an animated GIF.
The CMB light that we observes comes from a (roughly) two-dimensional surface intersecting this three-dimensional mixture of 150 Mpc spheres. Hence, as shown in Illustration 2, the pattern of the CMB is like adding up random slices of the BAO photon shell having random amplitudes. Because the amplitude of the over- and underdensities is very small—around 1 in 100,000—everything is nice and linear and so simply taking the superposition of these slices is quite valid.
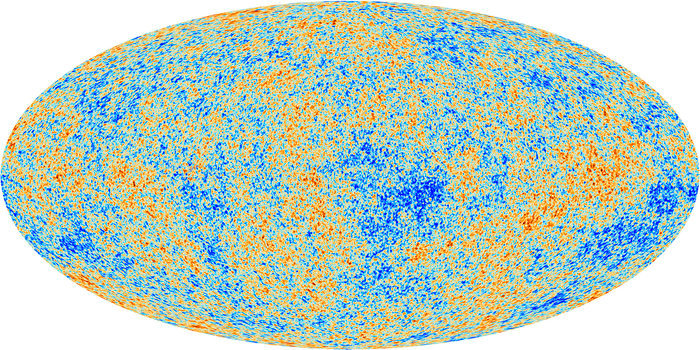
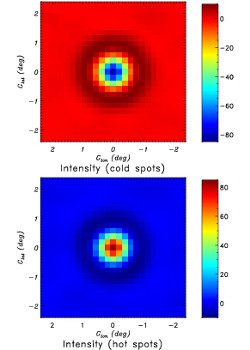
The actual CMB as measured by the Planck experiment. Left: the full-sky image of the CMB. Right: the BAO shell can be reconstructed by clipping out local maxima or minima (i.e., ‘hot spots’ or ‘cold spots’) and stacking them together. The result is approximately what you would get by adding up lots of random slices of the shells plotted in Illustration 1, i.e., the result if all the shells in Illustration 2 had been superimposed rather than randomly scattered.
Images: ESA and the Planck Collaboration – Planck 2013 Results I, Astron. Astrophys. 571 (2014).
Often, the CMB is analysed in spherical harmonic space—the, Fourier space of a sphere. The spherical harmonics have two dimensions: ℓ encodes the spatial size of a given mode, and m encodes its phase, i.e., its orientation on the sphere. Because the field of density fluctuations after inflation was random, the orientations of the spherical harmonic modes are also random, so no real physical information is encoded in the m dimension. Hence, the Fourier representation of the CMB pattern shown in the left panel of Illustration 3 can be collapsed along the m axis so that all the information is encoded in the spherical harmonic power as a function of ℓ alone. A heuristic way to think about this is that you get all the information about the CMB by taking the transform of the radial profile of the stacked image in the right panel of Illustration 3.
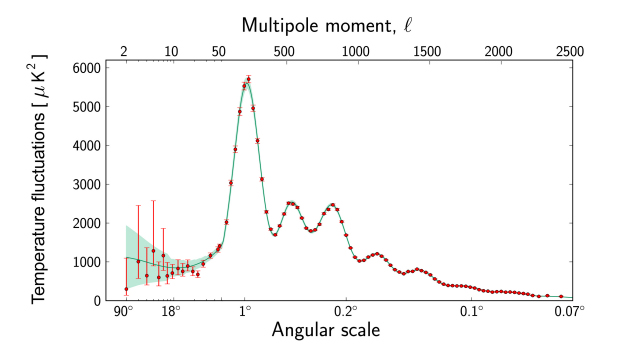
The angular power spectrum of the CMB temperature, as measured by Planck.
Image: ESA and the Planck Collaboration
Illustration 4 shows the power spectrum of CMB temperature fluctuations as measured by Planck. The most noticeable feature is the oscillatory pattern. This is in large part what the BAO feature looks like in Fourier space, and the position of the peaks depends on the size of the BAO shell. Analysing the locations and heights and the drop-off of of the oscillations provides a whole wealth of information about the relative amounts of the primordial components, about dark energy, the curvature of the Universe, and so on, none of which I will touch upon here.
However, I should mention that the cartoon-version of the CMB I have sketched above has some oversimplifications. Some of the other factors that affect the actual CMB pattern that is measured are:
- In Illustration 2, it is assumed that the transition of the baryons from being ionised to neutral is instantaneous. In reality, it took a finite amount of time. This means that the slices through the BAO had a non-infinitesimal thickness, thereby blurring the BAO feature. In the power spectrum, it reduces the contrast in the BAO harmonics.
- In addition to the density of the photons themselves when they decouple, temperature variations are caused by gravitational red- and blueshifts and are hence sensitive to the dark matter distribution (since it dominates the density). Denser regions cool down the photons by stretching the wavelength and more rarified regions heat them up. This effect—called the Sachs-Wolfe effect—dominates only on scales larger than the BAO feature. In the power spectrum of Illustration 4, the Sachs-Wolfe effect is important at ℓ below about 50. The power spectrum is roughly flat here: what this is indicating is that the initial density perturbations really were random with no strongly-preferred length scale.
- On small scales, the photons weren't perfectly coupled to the baryons. They did have space to ‘bounce around’ as they scattered off of baryons. This means that on small scales (or large ℓ in the power spectrum), the distribution of photons and baryons was not strongly coupled.
- There is a lot of stuff between us and the epoch of decoupling, and it interacts with the CMB photons as they make their journey towards us. Gravitational lensing by large scale-structure distorts the shapes of the hot- and cold-spots slightly. The gas in clusters of galaxies scatters the CMB creating small, localised increases or decreases in the temperature (depending on the wavelength). Additionally, some types of galaxies emit lots of light at the wavelengths that we observe the CMB so that there are point-like sources superimposed. Finally, our own galaxy emits its own light and in many places in the sky this ‘contamination’ is not negligible.
- In fact, it is these secondary effects that the Atacama Cosmology Telescope, one of the projects in which I am involved, is designed to study. There is a lot to be learnt from these components of the CMB that don't come directly from BAO.
Baryon Acoustic Oscillations in the Distribution of Galaxies [⯅ Top]
Galaxies tend to form where the density of hydrogen and helium is higher, because these locations gravitationally attract surrounding material, which collapses until it starts forming stars. We don't know exactly when the first galaxies formed, but it was in the neighbourhood of one or two hundred million years after the CMB was released, or at a redshift of z = 6 or 7. If you look at Illustration 1 at this redshift, the density distribution of baryons and dark matter are roughly coincident by this time, and the BAO feature is still very much present.
As big as galaxies are, they are tiny compared to the size of the BAO scale. Our own galaxy is about 100,000 light-years across, but the BAO scale is about 500,000,000 light-years. Thus, the structure within individual galaxies isn't affected at all by BAO. But on huge length scales, the clustering of galaxies is a bit stronger on the BAO length scale.
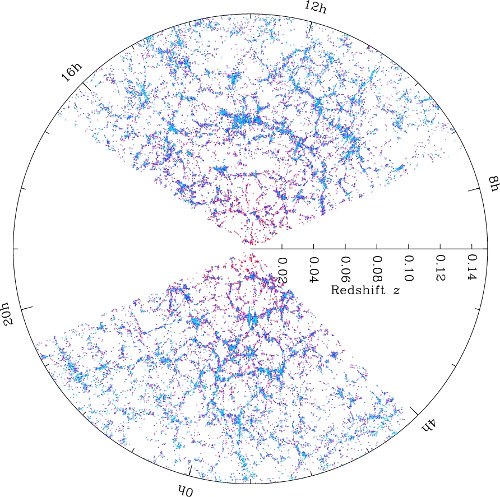
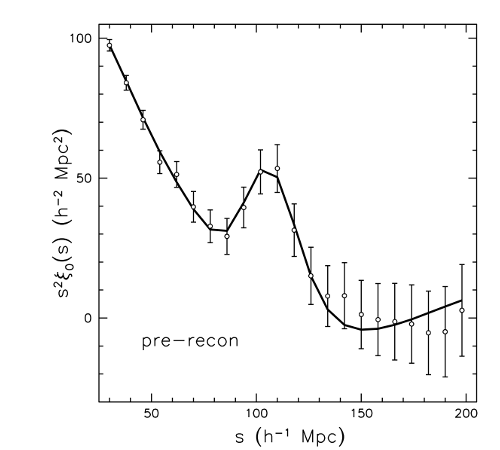
Left: a two-dimensional slice of the map of the Universe obtained by the Sloan Digital Sky Survey (SDSS). We are at the centre and the map extends about 2 billion light-years. Each dot is a single galaxy, and the blank parts are regions of the sky that SDSS did not observe. Right: the correlation function of the galaxy distribution, i.e., the relative number of galaxies one finds as a function of radius from a central point. This image can be compared to the BAO mass profile in the top-left plot of Illustration 1 at zero redshift.
Image: M. Blanton and the Sloan Digital Sky Survey (CC-BY-4.0). Plot: Anderson et al., MNRAS 441 (1), 24.
Illustration 5 shows the large-scale distribution of galaxies today, and how the BAO feature shows up when you look at how correlated the position of galaxies are as a function of their separation. This result, which has been demonstrated by several research groups, is an amazing example of how consistent our understanding of cosmology is. Using one physical model, we can explain the structure of the CMB fourteen billion years ago and connect that to how large-scale structure in today's Universe is arranged. And it has all been influenced by simple sound waves that began propagating in the first minutes of the Universe.
One powerful thing that BAO can be used for is measuring how fast the Universe is accelerating. This is what HIRAX and CHIME are aiming to do in an innovative new way—read more about them there.
Credits [⯅ Top]
The essential idea for this page was sparked by the now-old but still excellent collection of webpages and PDFs by Daniel Eisenstein and much of the presentation and information on this page was inspired by material there: in particular, the way of visualising the evolution of an overdensity in Illustration 1 and the conceptual framework for Illustration 2. Those pages have a lot more detailed information, including links to scientific papers, for further reading.
Credits for images and software are given in place above.